演算法第一講——Euclid Algorithm 歐幾里得演算法

大家在過往學習的經驗中，可能都有聽過歐幾里德這名鼎鼎大名的人物，是位在希臘化時期的數學家，有著著名著作「幾何原本」，在數學領域中有著極大化的貢獻，為現今眾多數學家所認同。

然而在古希臘的時代的數學家竟然能跟演算法畫上關係，畢竟演算法便是透過有限的步驟中，將給定的輸入做出最有效的解決，並且在執行玩這些有效的步驟中會有正當的終止，產生最後輸出結果，而歐幾里德演算法得以詮釋這些過程，歐幾里德演算法的問題是要在給定的兩個正整數 m 和 n 中找出兩束的最大公因數，因此我們可以列出以下解題步驟：

1. 找出餘數 (m % n)
2. 判斷餘數是否為零 (if (r = 0) return n)
3. 被除數與餘數互換 (swap(m, n))

那看到這邊可能人會有很多有很熟悉的感覺，畢竟我們曾經學習過求公因數的方法有：列舉法、質因數分解、短除法等⋯⋯那其中還有一個有趣的方法便是「輾轉相除法」，也就是我們今天要討論到的歐幾里德演算法，然而所謂的「輾轉」是什麼呢？可能是 Debug 睡不著的時候吧！哈！不過這樣也說得通，輾轉就是曲折的、不斷的過程，而我們正是透過這樣的特性來達成我們的演算法。

輾轉相除法直式

輾轉過程

過程以長方形圖是呈現

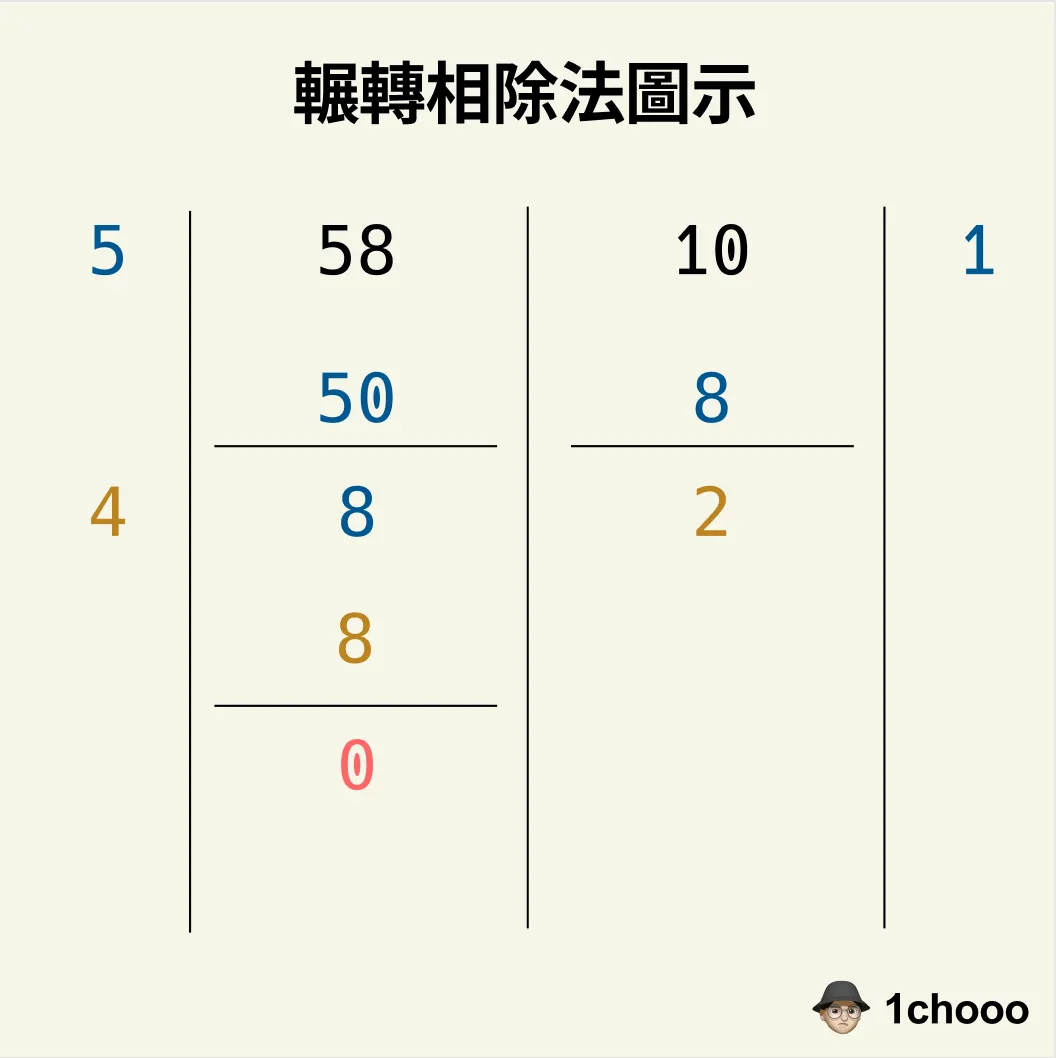
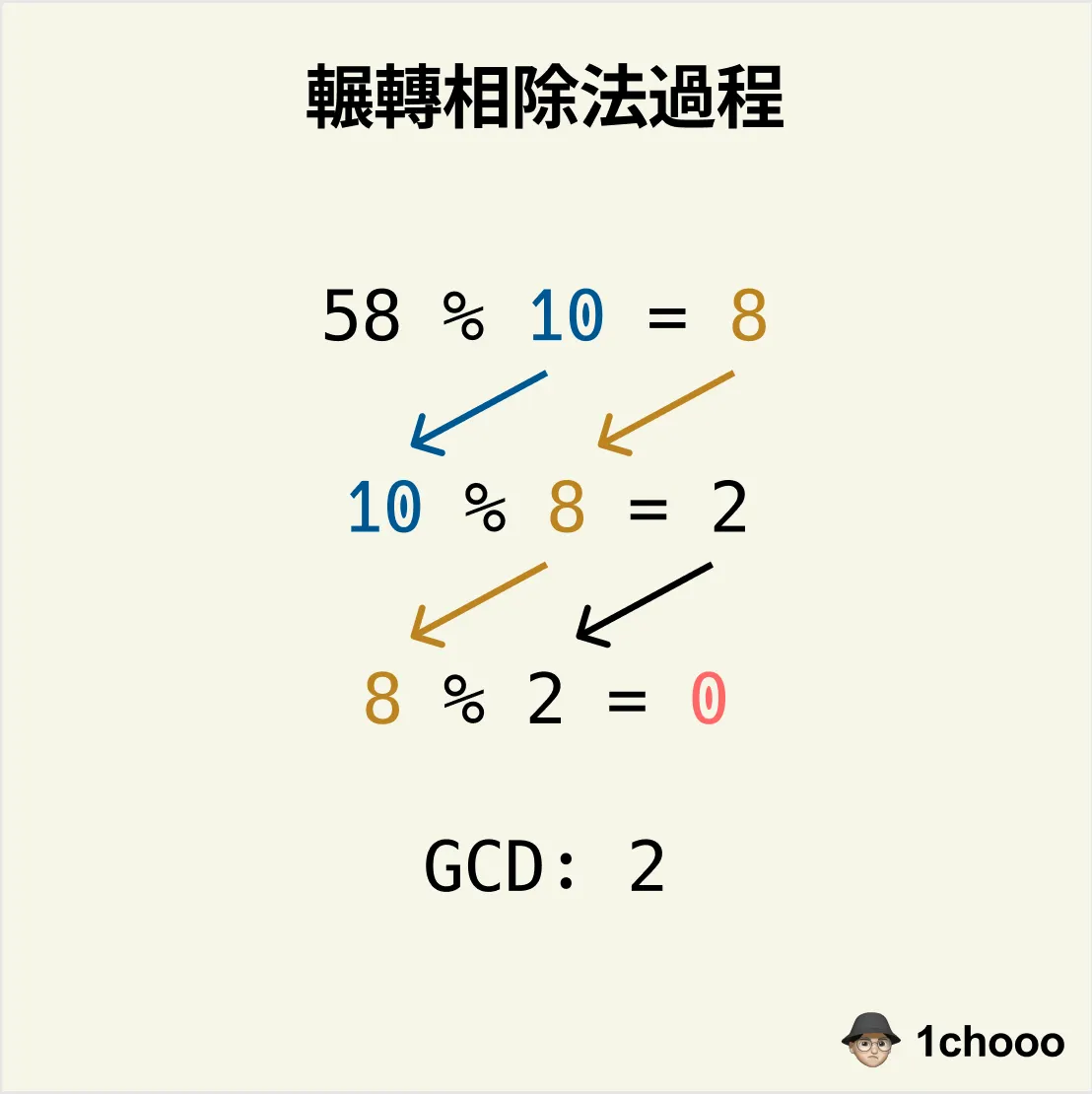
透過上方圖示我們便可看出輾轉的真正特性，透過互換且不斷地進行運算，已達到我們期望的結果，也可以從上圖中透過切割長方形的模式，在長方形中找出能切割的最大面積正方形，以此將整個長方形變成有正方形所組成的型態，這又可以回歸到上述所歸納的兩個解：

1. 餘數為 0 -> 完整地切割
2. 餘數為 1 -> 無法完整地切割

想必讀到這裡一定更能理解輾轉相除法，接下來我們進行實作吧！

以下我們展示虛擬碼 (Pseudocode)

Algorithm: EuclidGCD(m, n)
Input: Two integer m and n.
Output: The greatest common factor of m and n.
r <- m % n
while r != 0 do
    m <- n
    n <- r
    r <- m % n
return n
以下我們使用 cpp 實作
int EuclidGCD(int m, int n) {
    int r = m % n;
    while (r != 0) {
        m = n;
        n = r;
        r = m % n;
    }
    return n;
}

那上面我們討論到歐幾里德演算法的範疇實屬理論，那實際用途到底可以實現什麼情形呢？在分析這道問號題之前，我們可以再回想一下此演算法，最核心的就是要找出最大公因數，並且在由大化小的過程中，可以達成更有效率地轉換，畢竟是透過一系列輾轉的過程，所以其實輾轉相除法的應用層面非常廣，可以在密碼學、數學、計算機科學等⋯⋯領域做使用，甚至在音樂方面都能有實際上的應用，若想知道更多，網路上其實還有更多有趣的範例等著你們去挖掘呢！（維基百科下方的參考連結有超多有趣的例子！）

Reference

• 欧几里得与《几何原本》(上篇）
• 【演算法】歐幾里得算法 Euclidean Algorithm